Unit 4 solving quadratic equations homework 7 the quadratic formula – Unit 4: Solving Quadratic Equations Homework 7: The Quadratic Formula delves into the intricacies of quadratic equations, providing a comprehensive understanding of the methods used to solve them. This exploration begins with the quadratic formula, a powerful tool that can be applied to any quadratic equation, regardless of its complexity.
The quadratic formula is a mathematical equation that can be used to find the roots of a quadratic equation. A quadratic equation is an equation of the form ax^2 + bx + c = 0, where a, b, and c are real numbers and a ≠ 0. The quadratic formula is: x = (-b ± √(b^2 – 4ac)) / 2a.
1. The Quadratic Formula

The quadratic formula is a mathematical formula that can be used to solve quadratic equations. A quadratic equation is an equation that can be written in the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the unknown variable.
The quadratic formula is:
x = (-b ± √(b^2
4ac)) / 2a
To use the quadratic formula, you simply plug the values of a, b, and c into the formula and solve for x. For example, to solve the equation x^2 – 5x + 6 = 0, you would plug in a = 1, b = -5, and c = 6 into the quadratic formula:
x = (-(-5) ± √((-5)^2
4(1)(6))) / 2(1)
This gives you two solutions: x = 2 and x = 3.
The quadratic formula can be used to solve any quadratic equation, but it is important to note that it does have some limitations. For example, the quadratic formula cannot be used to solve equations that have complex solutions. Additionally, the quadratic formula can sometimes give extraneous solutions, which are solutions that do not satisfy the original equation.
2. Completing the Square
Completing the square is a method that can be used to solve quadratic equations. To complete the square, you first need to move the constant term to the other side of the equation. Then, you need to add and subtract the square of half the coefficient of the x-term to both sides of the equation.
For example, to solve the equation x^2 – 5x + 6 = 0, you would first move the constant term to the other side of the equation:
x^2
- 5x =
- 6
Then, you would add and subtract the square of half the coefficient of the x-term, which is 5/2, to both sides of the equation:
x^2
- 5x + (5/2)^2 =
- 6 + (5/2)^2
This gives you the following equation:
(x
5/2)^2 = 1/4
You can now take the square root of both sides of the equation to solve for x:
x
5/2 = ±1/2
This gives you two solutions: x = 2 and x = 3.
Completing the square can be used to solve any quadratic equation, but it is often easier to use the quadratic formula.
3. Factoring
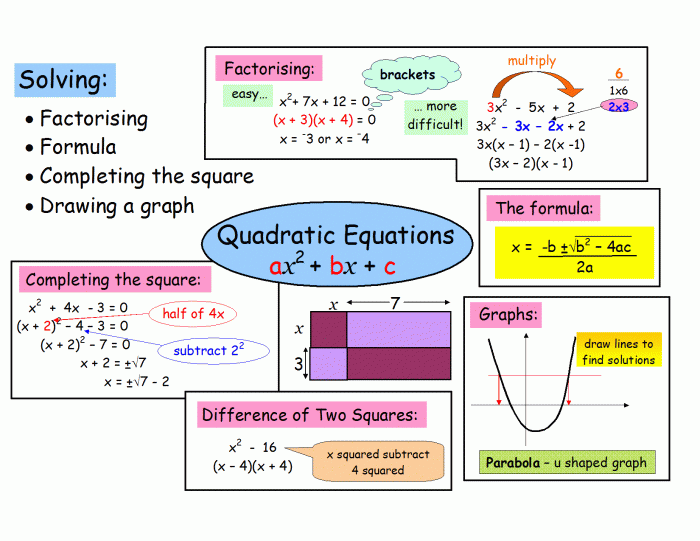
Factoring is a method that can be used to solve quadratic equations. To factor a quadratic equation, you need to find two numbers that add up to the coefficient of the x-term and multiply to the constant term.
For example, to factor the equation x^2 – 5x + 6 = 0, you need to find two numbers that add up to -5 and multiply to 6. These numbers are -2 and – 3. Therefore, you can factor the equation as follows:
x^2
- 5x + 6 = (x
- 2)(x
- 3)
You can now solve the equation by setting each factor equal to zero:
x
- 2 = 0 or x
- 3 = 0
This gives you two solutions: x = 2 and x = 3.
Factoring can be used to solve any quadratic equation, but it is only possible if the equation can be factored into two linear factors.
4. The Quadratic Formula Table
The quadratic formula table is a table that summarizes the different methods that can be used to solve quadratic equations. The table includes the steps involved in each method and examples of how to use the method.
| Method | Steps | Example |
|---|---|---|
| Quadratic Formula | 1. Plug the values of a, b, and c into the quadratic formula.
|
x = (-(-5) ± √((-5)^2
|
| Completing the Square | 1. Move the constant term to the other side of the equation.
|
x
x = 2, 3 |
| Factoring | 1. Find two numbers that add up to the coefficient of the x-term and multiply to the constant term.
|
x^2
x = 2, 3 |
5. Applications of Quadratic Equations: Unit 4 Solving Quadratic Equations Homework 7 The Quadratic Formula

Quadratic equations have many applications in real-world problems. For example, quadratic equations can be used to solve problems in physics, engineering, and other fields.
One example of how quadratic equations can be used to solve problems in physics is in the study of projectile motion. The equation for projectile motion is:
h =
16t^2 + vt + h0
where h is the height of the projectile, t is the time, v is the initial velocity, and h0 is the initial height.
This equation can be used to solve problems such as finding the maximum height of a projectile or the time it takes for a projectile to hit the ground.
Another example of how quadratic equations can be used to solve problems in engineering is in the design of bridges and other structures. The equation for the deflection of a beam is:
y =
wL^4 / (8EI)
where y is the deflection, w is the load, L is the length of the beam, E is the modulus of elasticity, and I is the moment of inertia.
This equation can be used to solve problems such as finding the maximum deflection of a beam or the load that a beam can support.
Q&A
What is the quadratic formula?
The quadratic formula is a mathematical equation that can be used to find the roots of a quadratic equation. It is: x = (-b ± √(b^2 – 4ac)) / 2a.
How do I use the quadratic formula?
To use the quadratic formula, you need to know the values of a, b, and c in the quadratic equation ax^2 + bx + c = 0. Once you have these values, you can plug them into the formula and solve for x.
What are the limitations of the quadratic formula?
The quadratic formula cannot be used to solve all quadratic equations. For example, it cannot be used to solve equations that have complex roots.